이 문제는 N<15이기 때문에, 제한시간 내에 백트래킹으로 해결할 수 있다.
첫번째로 퀸의 움직임을 이해하고 시뮬레이션을 돌려보자.
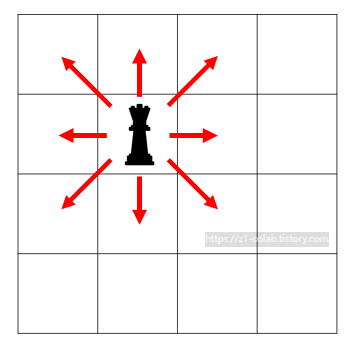
퀸은 위의 그림처럼 상하좌우, 대각선으로 움직일 수 있다.
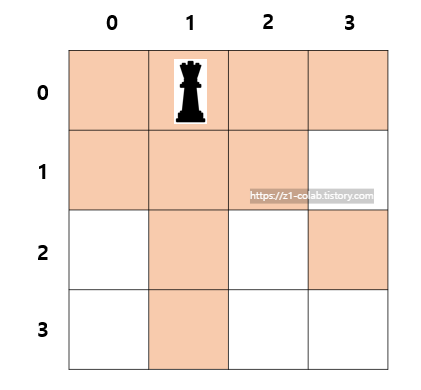
따라서 그림과 같이 (0,1)에 퀸이 위치한다고 했을 때, 주황색 칸을 제외한 칸에만 다음 퀸이 위치할 수 있다.
이 때 가장 먼저 알아차릴 수 있는 특징은 한 행에는 한 개의 퀸만 위치할 수 있다는 것이다.
따라서 k번째 퀸을 위치시킬 때는 k번째 열만 확인하면 된다.
그렇다면 각 열과 대각선의 점유 상태를 어떻게 체크할 수 있을까?
k번째 퀸을 놓을 때, for문을 돌며 앞서 놓은 퀸의 위치에 따라 칸들을 제외시킬 수도 있겠지만,
매우 비효율적이다.
다시 한 번 생각해보자.
k번째 놓일 퀸은 이전에 놓인 퀸들과 같은 '열'에 놓일 수 없다.
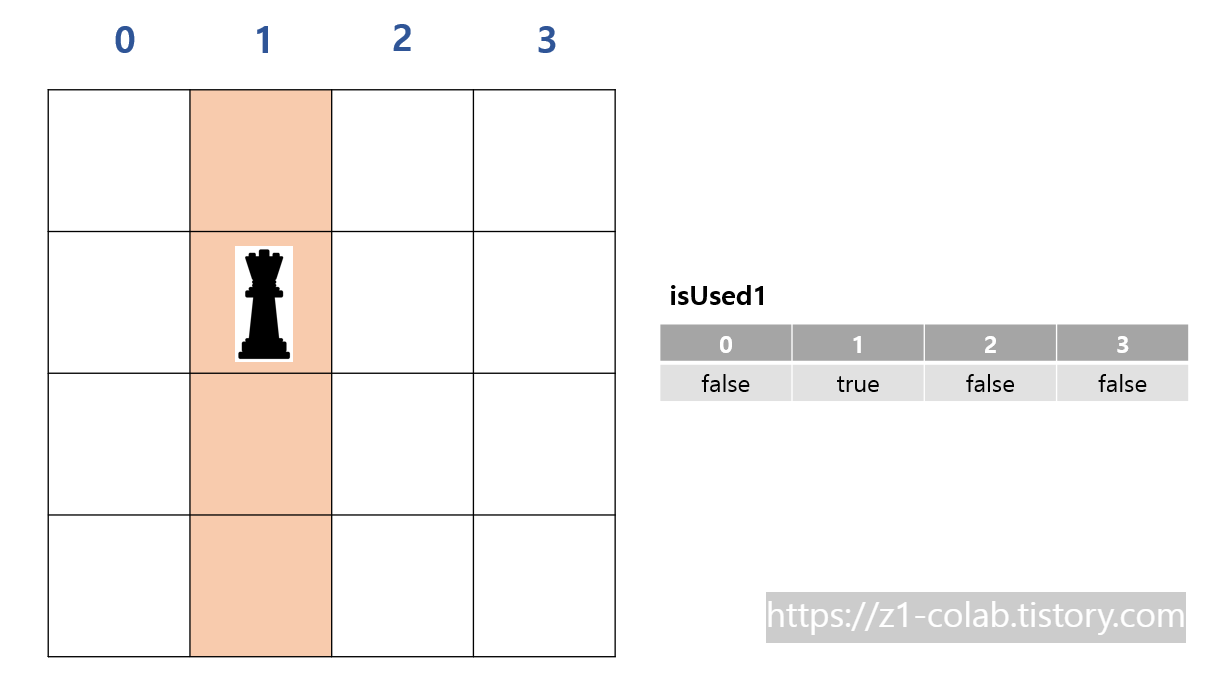
열의 점유 상태를 기록하는 bool isUsed1을 통해 어떤 열에 더이상 퀸을 놓을 수 없는지 알 수 있다.
또한 이전의 퀸들과 같은 대각선을 공유할 수 없다.
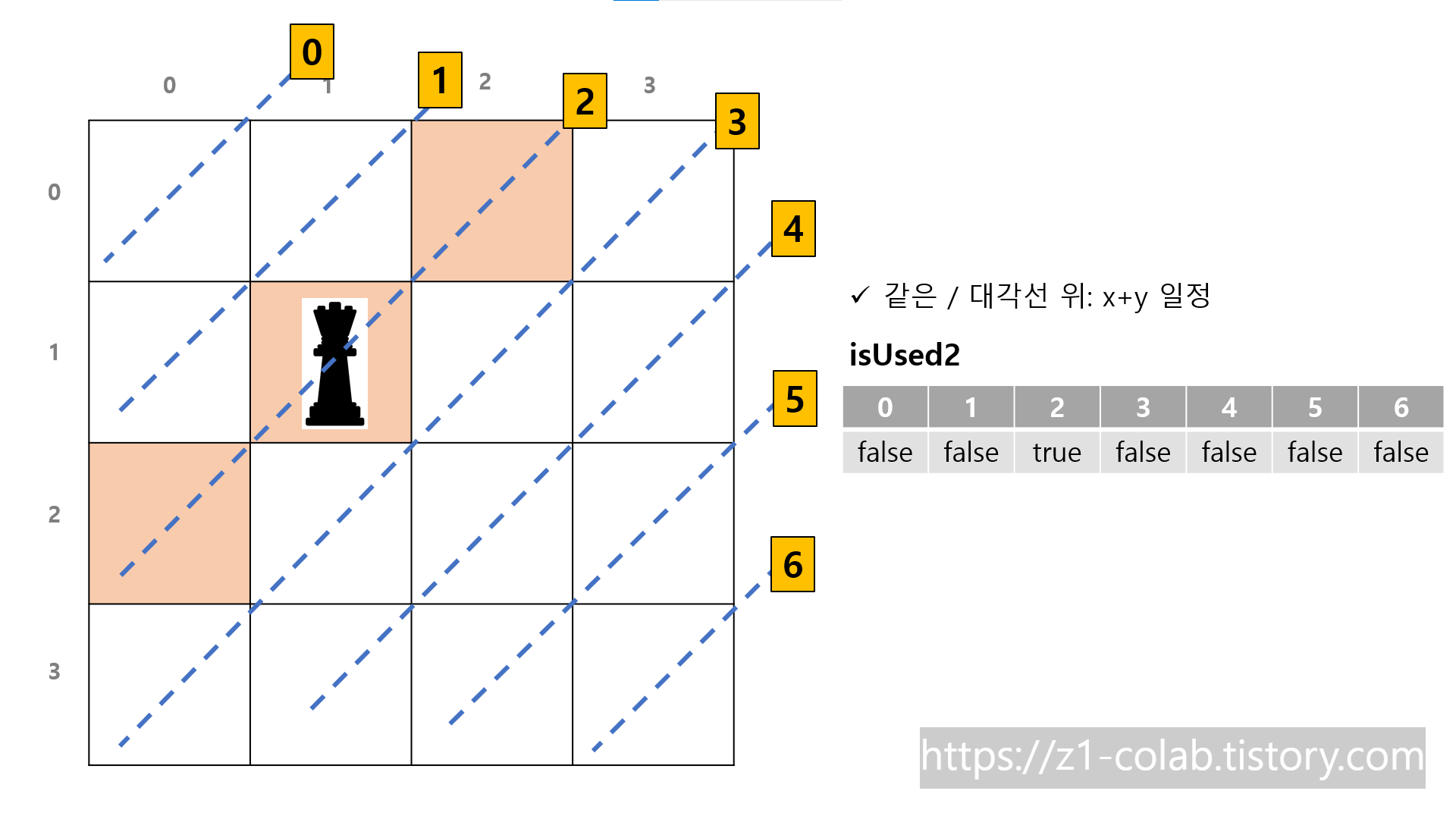
오른쪽 위를 향하는 대각선 위에 있는 칸들은 모두 x+y값이 같다.
오른쪽 위를 향하는 대각선의 점유 상태를 bool isUsed2에 기록한다.
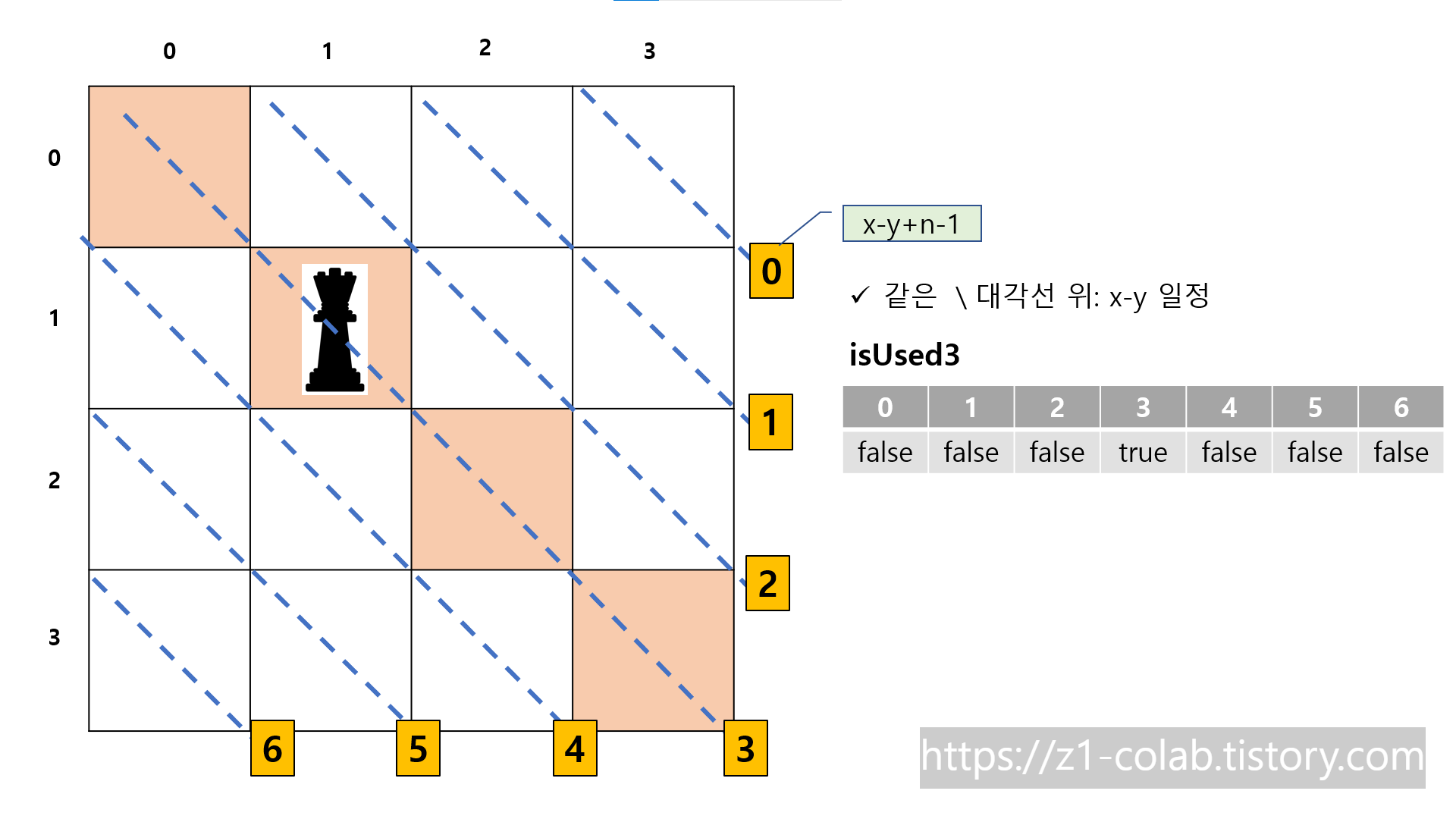
오른쪽 아래를 향하는 대각선 위에 있는 칸들은 모두 x-y값이 같다.
오른쪽 위를 향하는 대각선의 점유 상태를 bool isUsed3에 기록한다.
isUsed3의 index는 x-y+n-1로 계산한다.
위의 과정을 토대로 코드를 짜보았다.
//2023-08-26.
/**
* 여러 번 복습하기
* isUsed를 두어 각 열과 대각선의 점유상태를 기록할 수 있다.
*/
#include "bits/stdc++.h"
using namespace std;
int n, cnt;
bool isUsed1[15]; //열 점유상태
bool isUsed2[29]; // /대각선
bool isUsed3[29]; // \대각선
void func(int k) { //한 행에 퀸 하나만 놓을 수 있음. k번째 행에 퀸을 놓을 차례
if (k == n) {
cnt++;
return;
}
for (int i = 0; i < n; i++) { //열
//이미 점유된 라인에 있는 열은 제외
if (isUsed1[i] || isUsed2[k + i] || isUsed3[k - i + n - 1]) continue;
//k번째 퀸이 점유하게 되는 영역 표시
isUsed1[i] = 1;
isUsed2[k + i] = 1;
isUsed3[k - i + n - 1] = 1;
func(k + 1);
//k번째 퀸이 i, j일때 모든 경우의 수를 다 확인했기 때문에 이전 상태로 되돌린다.
isUsed1[i] = 0;
isUsed2[k + i] = 0;
isUsed3[k - i + n - 1] = 0;
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
func(0);
cout << cnt;
}
바킹독-백트래킹 강의를 참고하였습니다.
'알고리즘 > 백준' 카테고리의 다른 글
| [BOJ]1182번: 부분수열의 합 (0) | 2023.08.26 |
|---|
